Basics of desdeo-emo¶
[ ]:
import plotly.graph_objects as go
import numpy as np
import pandas as pd
from desdeo_problem import variable_builder, ScalarObjective, MOProblem
from desdeo_problem.testproblems.TestProblems import test_problem_builder
from desdeo_emo.EAs.NSGAIII import NSGAIII
from desdeo_emo.EAs.RVEA import RVEA
from desdeo_emo.utilities.plotlyanimate import animate_init_, animate_next_
Define objective functions¶
[2]:
def f_1(x):
term1 = ((x[:,0] - 2) ** 2) / 2
term2 = ((x[:,1] + 1) ** 2) / 13
return term1 + term2 + 3
def f_2(x):
term1 = ((x[:, 0] + x[:, 1] - 3) ** 2) / 36
term2 = ((-x[:, 0] + x[:, 1] + 2) ** 2) / 8
return term1 + term2 - 17
def f_3(x):
term1 = ((x[:, 0] + (2 * x[:, 1]) - 1) ** 2) / 175
term2 = ((-x[:, 0] + 2* x[:, 1]) ** 2) / 17
return term1 + term2 - 13
Note that the expected input x is two dimensional. It should be a 2-D numpy array.
Create Variable objects¶
[3]:
help(variable_builder)
Help on function variable_builder in module desdeo_problem.problem.Variable:
variable_builder(names: List[str], initial_values: Union[List[float], numpy.ndarray], lower_bounds: Union[List[float], numpy.ndarray] = None, upper_bounds: Union[List[float], numpy.ndarray] = None) -> List[desdeo_problem.problem.Variable.Variable]
Automatically build all variable objects.
Args:
names (List[str]): Names of the variables
initial_values (np.ndarray): Initial values taken by the variables.
lower_bounds (Union[List[float], np.ndarray], optional): Lower bounds of the
variables. If None, it defaults to negative infinity. Defaults to None.
upper_bounds (Union[List[float], np.ndarray], optional): Upper bounds of the
variables. If None, it defaults to positive infinity. Defaults to None.
Raises:
VariableError: Lengths of the input arrays are different.
Returns:
List[Variable]: List of variable objects
[4]:
list_vars = variable_builder(['x', 'y'],
initial_values = [0,0],
lower_bounds=[-400, -400],
upper_bounds=[400, 400])
list_vars
[4]:
[<desdeo_problem.problem.Variable.Variable at 0x1fe27917448>,
<desdeo_problem.problem.Variable.Variable at 0x1fe27917488>]
Create Objective objects¶
[5]:
f1 = ScalarObjective(name='f1', evaluator=f_1)
f2 = ScalarObjective(name='f2', evaluator=f_2)
f3 = ScalarObjective(name='f3', evaluator=f_3)
list_objs = [f1, f2, f3]
Create the problem object¶
[6]:
problem = MOProblem(variables=list_vars, objectives=list_objs)
Using the EAs¶
Pass the problem object to the EA, pass parameters as arguments if required.
[7]:
help(NSGAIII)
Help on class NSGAIII in module desdeo_emo.EAs.NSGAIII:
class NSGAIII(desdeo_emo.EAs.BaseEA.BaseDecompositionEA)
| NSGAIII(problem: desdeo_problem.problem.Problem.MOProblem, population_size: int = None, population_params: Dict = None, n_survive: int = None, initial_population: desdeo_emo.population.Population.Population = None, lattice_resolution: int = None, selection_type: str = None, a_priori: bool = False, interact: bool = False, use_surrogates: bool = False, n_iterations: int = 10, n_gen_per_iter: int = 100, total_function_evaluations: int = 0)
|
| Python Implementation of NSGA-III. Based on the pymoo package.
|
| Most of the relevant code is contained in the super class. This class just assigns
| the NSGAIII selection operator to BaseDecompositionEA.
|
| Parameters
| ----------
| problem : MOProblem
| The problem class object specifying the details of the problem.
| population_size : int, optional
| The desired population size, by default None, which sets up a default value
| of population size depending upon the dimensionaly of the problem.
| population_params : Dict, optional
| The parameters for the population class, by default None. See
| desdeo_emo.population.Population for more details.
| initial_population : Population, optional
| An initial population class, by default None. Use this if you want to set up
| a specific starting population, such as when the output of one EA is to be
| used as the input of another.
| lattice_resolution : int, optional
| The number of divisions along individual axes in the objective space to be
| used while creating the reference vector lattice by the simplex lattice
| design. By default None
| selection_type : str, optional
| One of ["mean", "optimistic", "robust"]. To be used in data-driven optimization.
| To be used only with surrogate models which return an "uncertainity" factor.
| Using "mean" is equivalent to using the mean predicted values from the surrogate
| models and is the default case.
| Using "optimistic" results in using (mean - uncertainity) values from the
| the surrogate models as the predicted value (in case of minimization). It is
| (mean + uncertainity for maximization).
| Using "robust" is the opposite of using "optimistic".
| a_priori : bool, optional
| A bool variable defining whether a priori preference is to be used or not.
| By default False
| interact : bool, optional
| A bool variable defining whether interactive preference is to be used or
| not. By default False
| n_iterations : int, optional
| The total number of iterations to be run, by default 10. This is not a hard
| limit and is only used for an internal counter.
| n_gen_per_iter : int, optional
| The total number of generations in an iteration to be run, by default 100.
| This is not a hard limit and is only used for an internal counter.
| total_function_evaluations :int, optional
| Set an upper limit to the total number of function evaluations. When set to
| zero, this argument is ignored and other termination criteria are used.
|
| Method resolution order:
| NSGAIII
| desdeo_emo.EAs.BaseEA.BaseDecompositionEA
| desdeo_emo.EAs.BaseEA.BaseEA
| builtins.object
|
| Methods defined here:
|
| __init__(self, problem: desdeo_problem.problem.Problem.MOProblem, population_size: int = None, population_params: Dict = None, n_survive: int = None, initial_population: desdeo_emo.population.Population.Population = None, lattice_resolution: int = None, selection_type: str = None, a_priori: bool = False, interact: bool = False, use_surrogates: bool = False, n_iterations: int = 10, n_gen_per_iter: int = 100, total_function_evaluations: int = 0)
| Initialize EA here. Set up parameters, create EA specific objects.
|
| ----------------------------------------------------------------------
| Methods inherited from desdeo_emo.EAs.BaseEA.BaseDecompositionEA:
|
| end(self)
| Conducts non-dominated sorting at the end of the evolution process
|
| Returns:
| tuple: The first element is a 2-D array of the decision vectors of the non-dominated solutions.
| The second element is a 2-D array of the corresponding objective values.
|
| manage_preferences(self, preference=None)
| Run the interruption phase of EA.
|
| Use this phase to make changes to RVEA.params or other objects.
| Updates Reference Vectors (adaptation), conducts interaction with the user.
|
| request_plot(self) -> desdeo_tools.interaction.request.SimplePlotRequest
|
| request_preferences(self) -> Union[NoneType, Tuple[desdeo_tools.interaction.request.PreferredSolutionPreference, desdeo_tools.interaction.request.NonPreferredSolutionPreference, desdeo_tools.interaction.request.ReferencePointPreference, desdeo_tools.interaction.request.BoundPreference]]
|
| requests(self) -> Tuple
|
| ----------------------------------------------------------------------
| Methods inherited from desdeo_emo.EAs.BaseEA.BaseEA:
|
| check_FE_count(self) -> bool
| Checks whether termination criteria via function evaluation count has been
| met or not.
|
| Returns:
| bool: True is function evaluation count limit NOT met.
|
| continue_evolution(self) -> bool
| Checks whether the current iteration should be continued or not.
|
| continue_iteration(self)
| Checks whether the current iteration should be continued or not.
|
| iterate(self, preference=None) -> Tuple
| Run one iteration of EA.
|
| One iteration consists of a constant or variable number of
| generations. This method leaves EA.params unchanged, except the current
| iteration count and gen count.
|
| start(self)
| Mimics the structure of the mcdm methods. Returns the request objects from self.retuests().
|
| ----------------------------------------------------------------------
| Data descriptors inherited from desdeo_emo.EAs.BaseEA.BaseEA:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
[8]:
evolver = NSGAIII(problem,
n_iterations=10,
n_gen_per_iter=100,
population_size=100)
[9]:
while evolver.continue_evolution():
evolver.iterate()
Extracting optimized decision variables and objective values¶
[10]:
individuals, solutions = evolver.end()
fig1 = go.Figure(
data=go.Scatter(
x=individuals[:,0],
y=individuals[:,1],
mode="markers"))
fig1
[11]:
fig2 = go.Figure(data=go.Scatter3d(x=solutions[:,0],
y=solutions[:,1],
z=solutions[:,2],
mode="markers",
marker_size=5))
fig2
[13]:
pd.DataFrame(solutions).to_csv("MOP7_true_front.csv")
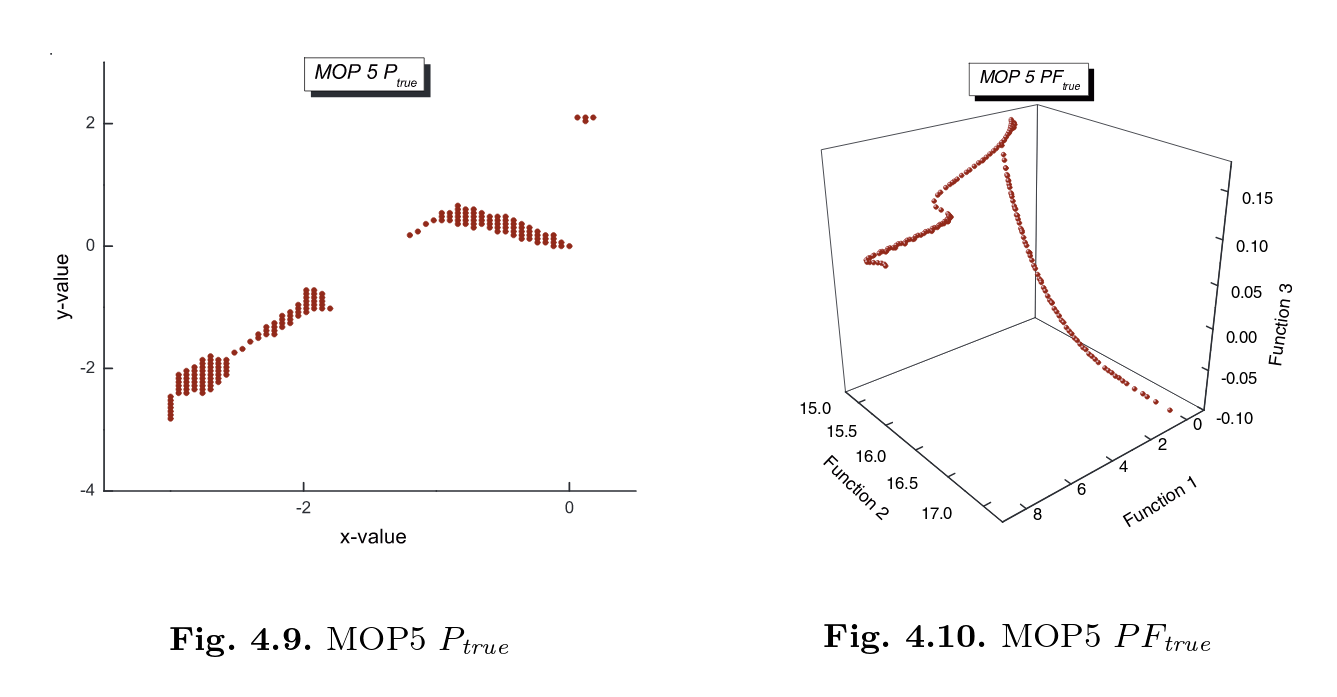
Coello MOP5¶
Definition¶
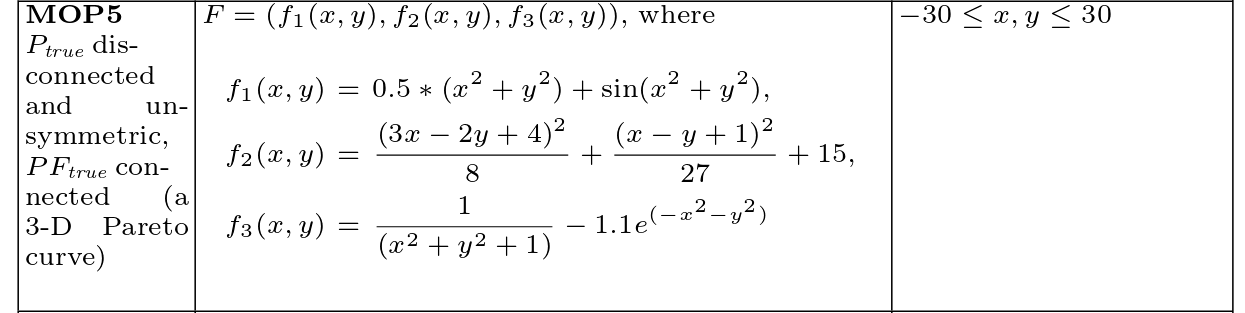
Pareto set and front¶
[14]:
def f_4(x):
term = x[:, 0]**2 + x[:, 1]**2
return 0.5*term + np.sin(term)
def f_5(x):
term1 = ((3*x[:, 0] - 2*x[:,1] + 4)**2)/8
term2 = ((x[:, 0] - x[:,1] + 1)**2)/27
return term1 + term2 + 15
def f_6(x):
term = x[:, 0]**2 + x[:, 1]**2
return (1/(term + 1)) - 1.1 * np.exp(-term)
[15]:
list_vars = variable_builder(['x', 'y'],
initial_values = [0,0],
lower_bounds=[-30, -30],
upper_bounds=[30, 30])
[16]:
f1 = ScalarObjective(name='f1', evaluator=f_4)
f2 = ScalarObjective(name='f2', evaluator=f_5)
f3 = ScalarObjective(name='f3', evaluator=f_6)
[17]:
problem = MOProblem(variables=list_vars, objectives=[f1, f2, f3])
[23]:
evolver = NSGAIII(problem)
[24]:
individual, solutions = evolver.end()
figure = animate_init_(solutions, filename="MOP5.html")
Plot saved as: MOP5.html
View the plot by opening the file in browser.
To view the plot in Jupyter Notebook, use the IFrame command.
Refresh the plot page after each iteration to get the updated animation¶
[25]:
while evolver.continue_evolution():
print(f"Running iteration {evolver._iteration_counter+1}")
evolver.iterate()
non_dominated = evolver.population.non_dominated_fitness()
figure = animate_next_(
evolver.population.objectives[non_dominated],
figure,
filename="MOP5.html",
generation=evolver._iteration_counter,
)
Running iteration 1
Running iteration 2
Running iteration 3
Running iteration 4
Running iteration 5
Running iteration 6
Running iteration 7
Running iteration 8
Running iteration 9
Running iteration 10
Interaction in EAs¶
The reference point method has been implemented.
[26]:
help(test_problem_builder)
Help on function test_problem_builder in module desdeo_problem.testproblems.TestProblems:
test_problem_builder(name: str, n_of_variables: int = None, n_of_objectives: int = None) -> desdeo_problem.problem.Problem.MOProblem
Build test problems. Currently supported: ZDT1-4, ZDT6, and DTLZ1-7.
Args:
name (str): Name of the problem in all caps. For example: "ZDT1", "DTLZ4", etc.
n_of_variables (int, optional): Number of variables. Required for DTLZ problems,
but can be skipped for ZDT problems as they only support one variable value.
n_of_objectives (int, optional): Required for DTLZ problems,
but can be skipped for ZDT problems as they only support one variable value.
Raises:
ProblemError: When one of many issues occur while building the MOProblem
instance.
Returns:
MOProblem: The test problem object
[27]:
problem = test_problem_builder(name="DTLZ1", n_of_variables=30, n_of_objectives=3)
[28]:
evolver = RVEA(problem, interact=True, n_iterations=5, n_gen_per_iter=400)
figure = animate_init_(
evolver.population.objectives[evolver.population.non_dominated_fitness()],
filename="dtlz1.html")
Plot saved as: dtlz1.html
View the plot by opening the file in browser.
To view the plot in Jupyter Notebook, use the IFrame command.
[29]:
pref, plot = evolver.start()
Loop over the following three cells, updating the preferences as desired¶
Try changing the preference once the Pareto front has been reached. Note the format of providing the preference. Check out the content of pref and plot
[30]:
print(pref[0].content['message'])
Please provide preferences. There is four ways to do this. You can either:
1: Select preferred solution(s)
2: Select non-preferred solution(s)
3: Specify a reference point worse than or equal to the ideal point
4: Specify desired ranges for objectives.
In case you choose
1, please specify index/indices of preferred solutions in a numpy array (indexing starts from 0).
For example:
numpy.array([1]), for choosing the solutions with index 1.
numpy.array([2, 4, 5, 16]), for choosing the solutions with indices 2, 4, 5, and 16.
2, please specify index/indices of non-preferred solutions in a numpy array (indexing starts from 0).
For example:
numpy.array([3]), for choosing the solutions with index 3.
numpy.array([1, 2]), for choosing the solutions with indices 1 and 2.
3, please provide a reference point worse than or equal to the ideal point:
f1 2.63548
f2 0.98086
f3 1.17816
Name: ideal, dtype: object
The reference point will be used to focus the reference vectors towards the preferred region.
If a reference point is not provided, the previous state of the reference vectors is used.
If the reference point is the same as the ideal point, the reference vectors are spread uniformly in the objective space.
4, please specify desired lower and upper bound for each objective, starting from
the first objective and ending with the last one. Please specify the bounds as a numpy array containing
lists, so that the first item of list is the lower bound and the second the upper bound, for each
objective.
For example: numpy.array([[1, 2], [2, 5], [0, 3.5]]), for problem with three objectives.
Ideal vector:
f1 2.63548
f2 0.98086
f3 1.17816
Name: ideal, dtype: object
Nadir vector:
f1 inf
f2 inf
f3 inf
Name: nadir, dtype: object.
[39]:
response = evolver.population.ideal_fitness_val + [0.5,0.7,0.1]
pref[2].response = pd.DataFrame([response], columns=pref[2].content['dimensions_data'].columns)
[40]:
pref, plot = evolver.iterate(pref[2])
figure = animate_next_(
plot.content['data'].values,
figure,
filename="dtlz1.html",
generation=evolver._iteration_counter,
)
message = (f"Current generation number:{evolver._current_gen_count}. "
f"Is looping back recommended: {'Yes' if evolver.continue_evolution() else 'No'}")
print(message)
Current generation number:2000. Is looping back recommended: No
[ ]:
